섬으로 이루어진 나라가 있고, 모든 섬을 다리로 연결하려고 한다. 이 나라의 지도는 N×M 크기의 이차원 격자로 나타낼 수 있고, 격자의 각 칸은 땅이거나 바다이다.
섬은 연결된 땅이 상하좌우로 붙어있는 덩어리를 말하고, 아래 그림은 네 개의 섬으로 이루어진 나라이다. 색칠되어있는 칸은 땅이다.
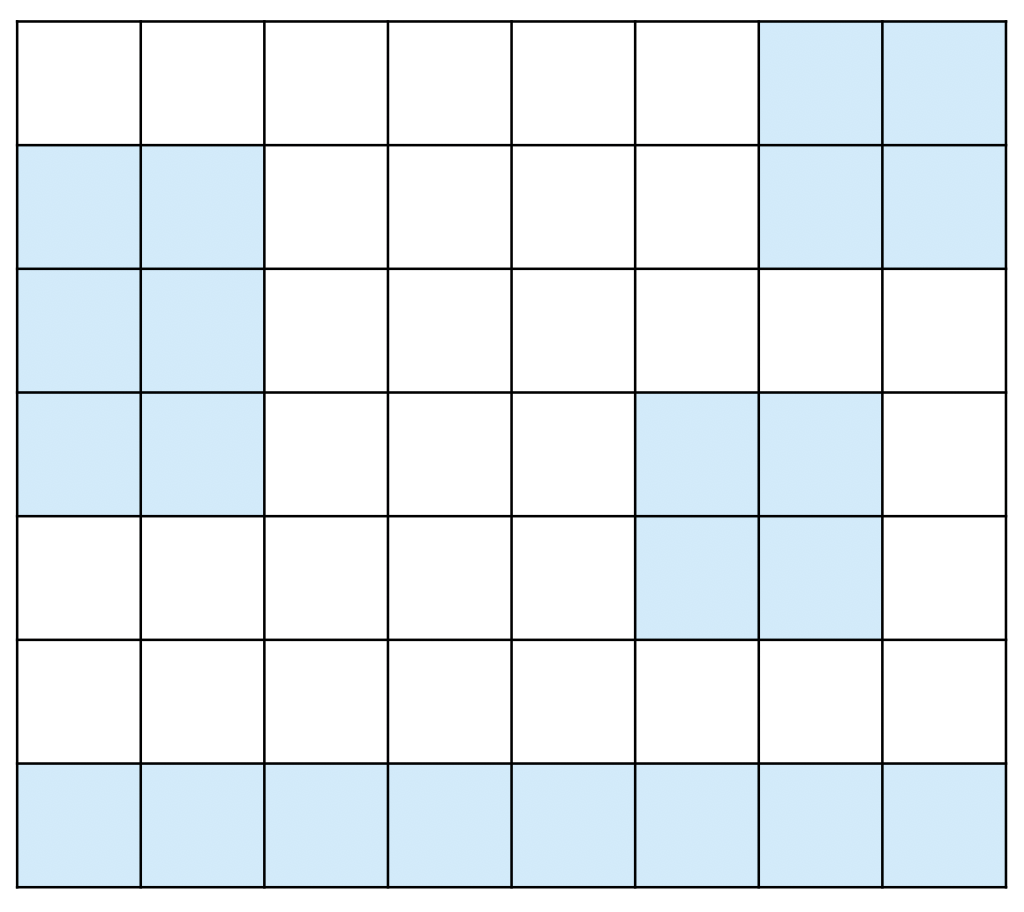
다리는 바다에만 건설할 수 있고, 다리의 길이는 다리가 격자에서 차지하는 칸의 수이다. 다리를 연결해서 모든 섬을 연결하려고 한다. 섬 A에서 다리를 통해 섬 B로 갈 수 있을 때, 섬 A와 B를 연결되었다고 한다. 다리의 양 끝은 섬과 인접한 바다 위에 있어야 하고, 한 다리의 방향이 중간에 바뀌면 안된다. 또, 다리의 길이는 2 이상이어야 한다.
다리의 방향이 중간에 바뀌면 안되기 때문에, 다리의 방향은 가로 또는 세로가 될 수 밖에 없다. 방향이 가로인 다리는 다리의 양 끝이 가로 방향으로 섬과 인접해야 하고, 방향이 세로인 다리는 다리의 양 끝이 세로 방향으로 섬과 인접해야 한다.
섬 A와 B를 연결하는 다리가 중간에 섬 C와 인접한 바다를 지나가는 경우에 섬 C는 A, B와 연결되어있는 것이 아니다.
아래 그림은 섬을 모두 연결하는 올바른 2가지 방법이고, 다리는 회색으로 색칠되어 있다. 섬은 정수, 다리는 알파벳 대문자로 구분했다.


다리가 교차하는 경우가 있을 수도 있다. 교차하는 다리의 길이를 계산할 때는 각 칸이 각 다리의 길이에 모두 포함되어야 한다.

나라의 정보가 주어졌을 때, 모든 섬을 연결하는 다리 길이의 최솟값을 구해보자.
입력
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.
출력
모든 섬을 연결하는 다리 길이의 최솟값을 출력한다. 모든 섬을 연결하는 것이 불가능하면 -1을 출력한다.
제한
- 1 ≤ N, M ≤ 10
- 3 ≤ N×M ≤ 100
- 2 ≤ 섬의 개수 ≤ 6
생각
최근 푼 문제중에 제일 어려웠던 문제이다..bfs/dfs에만 익숙해져 있어 이를 이용해 푸려고하니 모든 섬이 연결되어 있는 상황을 확인하는게 어려웠다.
각 섬(n개라고 하자)에서 연결할 수 있는 다리는 여러 개이고, 이들 중 n-1개의 다리를 골라 모두 이어지게 만들며 최소의 값을 구하는 문제이다. (n-1개의 다리를 선택해야 최소가 될 수 있다.)
위 문장을 다시 해석하면 n개의 노드가 있고, n-1개의 간선을 택하여 거리의 최솟값을 구한다.
즉, mst 최소 신장 트리이다!! 나는 상시테스트를 볼 때 크루스칼 알고리즘을 제대로 몰라 풀기가 어려웠다.
크루스칼 알고리즘을 모르겠는 사람은
[Java][자바][백준][1197번] 최소 스패닝 트리 - 크루스칼 알고리즘
문제 설명 그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오. 최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트..
ju-nam2.tistory.com
를 먼저 보고 오기를 추천한다!
과정은 다음과 같다.
1. 각 섬에 번호를 붙여준다. (섬을 구분하기 위함) bfs활용!
2. 각 좌표에서 최대로 만들 수 있는 다리를 모두 만들어 우선 순위 큐에 넣어준다. (크루스칼을 사용하기 위해 edge클래스를 만들어 Comparable를 implement해준다.)
3. 크루스칼 알고리즘을 통해 최소 간선의 합을 구해준다.
주석에 상세한 설명을 적도록 하겠다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
|
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
static int[] dx = {0,0,1,-1};
static int[] dy = {1,-1,0,0};
static int n,m;
static int[][] map;
static boolean[][] visited;
static int island = 0;
static PriorityQueue<edge> pq = new PriorityQueue<edge>();
static int result = 0;
static int[] parents;
static int bridge_count = 0;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] str = br.readLine().split(" ");
n = Integer.parseInt(str[0]);
m = Integer.parseInt(str[1]);
map = new int[n][m];
visited = new boolean[n][m];
for(int i=0; i<n; i++) {
str = br.readLine().split(" ");
for(int j=0; j<m; j++) {
map[i][j] = Integer.parseInt(str[j]);
}
}
//bfs를 통해 섬에 번호를 부여한다.
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
if(map[i][j] == 1 && !visited[i][j]) {
island++;
bfs(new dot(i,j));
}
}
}
//각 좌표에서 만들 수 있는 최대의 다리를 만든다.
//다리의 길이는 2이상이어야 하므로, 2 이상이면 pq에 넣어준다.
visited = new boolean[n][m];
//show();
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
if(map[i][j] != 0) {
makeBridge(new dot(i,j), map[i][j]);
}
}
}
//다리를 다 만들었으면 크루스칼 알고리즘을 실행한다.
//pq의 간선만큼 반복하면서 사이클을 확인하며 최소 간선의 합을 구한다.
parents = new int[island+1];
for(int i=0; i<parents.length; i++) {
parents[i] = i;
}
int size = pq.size();
for(int i=0; i<size; i++) {
edge tmp = pq.poll();
int a = find(tmp.s);
int b = find(tmp.e);
if(a==b) continue;
union(tmp.s, tmp.e);
result += tmp.v;
bridge_count++;
}
//result == 0 이거나 다리의 개수가 섬의 개수 - 1이 아니면 -1을 출력한다.
if(result == 0 || bridge_count != island-1) {
System.out.println(-1);
} else {
System.out.println(result);
}
}
static void bfs(dot d) {
Queue<dot> q = new LinkedList<dot>();
visited[d.x][d.y] = true;
map[d.x][d.y] = island;
q.add(d);
while(!q.isEmpty()) {
dot t = q.poll();
int x = t.x;
int y = t.y;
for(int i=0; i<4; i++) {
int x2 = x + dx[i];
int y2 = y + dy[i];
if(x2>=0 && x2<n && y2>=0 && y2<m && map[x2][y2] == 1 && !visited[x2][y2]) {
q.add(new dot(x2,y2));
map[x2][y2] = island;
visited[x2][y2] = true;
}
}
}
}
//상하좌우 중 한 방향으로 계속 이동하면서 다른 섬이 나올 때까지 반복한다.
//중간에 좌표를 넘어가거나, 자신과 같은 번호가 나오면 좌표와 length를 초기화 한후 넘어간다.
public static void makeBridge(dot d, int num) {
int x2 = d.x;
int y2 = d.y;
int length = 0;
for(int i=0; i<4; i++) {
while(true) {
x2 = x2 + dx[i];
y2 = y2 + dy[i];
if(x2>=0 && x2<n && y2>=0 && y2<m) {
if(map[x2][y2] == num) {
length = 0;
x2 = d.x;
y2 = d.y;
break;
} else if(map[x2][y2] == 0){
length++;
} else {
//1보다 크면 pq에 추가해준다.
if(length > 1) {
pq.add(new edge(num, map[x2][y2], length));
}
length = 0;
x2 = d.x;
y2 = d.y;
break;
}
} else {
length = 0;
x2 = d.x;
y2 = d.y;
break;
}
}
}
}
//크루스칼 알고리즘을 위한 find, union 함수.
//외우는게 편하다
public static int find(int a) {
if(a == parents[a]) return a;
parents[a] = find(parents[a]);
return parents[a];
}
public static void union(int s,int e) {
int aRoot = find(s);
int bRoot = find(e);
if(aRoot != bRoot) {
parents[aRoot] = e;
} else {
return;
}
}
}
class dot {
int x;
int y;
public dot(int x,int y) {
this.x = x;
this.y = y ;
}
}
// 간선 class : value를 기준으로 compareTo를 overriding하였다.
class edge implements Comparable<edge> {
int s;
int e;
int v;
public edge(int s,int e,int v) {
super();
this.s = s;
this.e = e;
this.v = v;
}
@Override
public int compareTo(edge arg0) {
return arg0.v >= this.v ? -1:1;
}
}
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
'알고리즘 > 코딩 - 백준' 카테고리의 다른 글
| [Java][자바][백준][17143번] 낚시왕 (2) | 2020.04.22 |
|---|---|
| [Java][자바][백준][16234번] 인구이동 (3) | 2019.11.28 |
| [Java][자바][백준][17471번] 게리맨더링 (0) | 2019.11.23 |
| [Java][자바][백준][17142번] 연구소 3 (0) | 2019.11.22 |
| [Java][자바][백준][11559번] Puyo Puyo (1) | 2019.11.20 |

